【2.3】参数估计基础(置信区间)

一、参数估计的概念

统计推断包括参数估计和假设检验。参数估计就是用样本指标（统计量）来评估总体指标（参数）。

参数估计：

• 点估计（point estimation）
• 区间估计（interval estimation）

1. 点估计

用样本统计量直接作为总体参数的估计值。

例如 于2000年测得某地27例健康成年男性血红蛋白量的 样本均数为125g/L，试估计其总体均数。 $$\bar X \ {\xrightarrow {}} \mu $$ ，即认为2000年该地所有健康成年男性血红蛋白 量的总体均数为125g/L 。

2.区间估计

• 按预先给定的概率(1-α) 估计总体参数的可能范围，该范围 就称为总体参数的1-α置信区间(confidence interval, CI) 。
• 预先给定的概率(1-α)称为置信度，常取95%或99%。如无 特别说明，一般取双侧95%。
• 置信区间由两个数值即置信限(下限和上限)构成

二、总体均数的区间估计

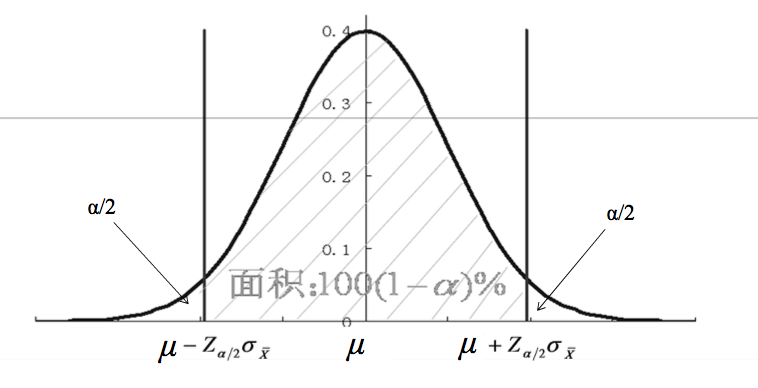
1. 总体均数置信区间的计算

1.σ已知

按标准正态分布原理计算，由Z分布，标准正态曲线下有95%的 Z 值在±1.96之间。

$$-1.96 < {\frac{\bar X - \mu}{\sigma_{\bar X}}} <1.96$$

$$\bar X - 1.96 \sigma_{\bar X} < \mu < \bar X + 1.96 \sigma_{\bar X}$$

95%的双侧置信区间:

$$ \left(\bar X - 1.96 \sigma_{\bar X} , \bar X + 1.96 \sigma_{\bar X} \right)$$

99%的双侧置信区间: $$ \left(\bar X - 2.58 \sigma_{\bar X} , \bar X + 2.58 \sigma_{\bar X} \right)$$

通式: $$\bar X ± z_{\alpha / 2}\sigma_{\bar X}$$ （双侧）

2.σ未知，但样本例数n足够大（n>50）时

由 t 分布可知，自由度越大，t 分布越逼近标准正态分布，此时 t 曲线下约有95%的 t 值在±1.96之间，即

$$-1.96 < {\frac{\bar X - \mu}{S_{\bar X}}} <1.96$$

$$\bar X - 1.96 S_{\bar X} < \mu < \bar X + 1.96 S_{\bar X}$$

95%的双侧置信区间:

$$ \left(\bar X - 1.96 S_{\bar X} , \bar X + 1.96 S_{\bar X} \right)$$

99%的双侧置信区间: $$ \left(\bar X - 2.58 S_{\bar X} , \bar X + 2.58 S_{\bar X} \right)$$

通式: $$\bar X ± z_{\alpha / 2}S_{\bar X}$$ （双侧）

例1：某市2000年随机测量了90名19岁健康男大学生的身高，其均 数为172.2cm，标准差为4.5cm,，试估计该地19岁健康男大学生的 身高的95%置信区间

$$\bar X ± z_{\alpha / 2}S_{\bar X}$$

$$ Z_{\alpha / 2} = 1.96$$

$$\bar X ± 1.96 S_{X} = 1.72 ±1.96 {\frac{4.5}{\sqrt{90}}} = \left(1.71.3,173.1\right) $$

该市19岁健康男大学生的身高的95%置信区间 (171.3,173.1) cm。

3.σ未知，但样本例数n较小

按t分布原理，此时某自由度的t曲线下约有95%的t值在 ±t_0.05/2(v)

$$-t_{0.05/2(v)}< t <t_{0.05/2(v)}$$ $$ -t_{0.05/2(v)}< {\frac{\bar X - \mu}{S_{\bar X}}} <t_{0.05/2(v)}$$ $$ \bar X - t_{0.05/2(v)}S_{\bar X} < \mu < \bar X + t_{0.05/2(v)}S_{\bar X} $$

95%的双侧置信区间: $$ \left(\bar X - t_{0.05/2(v)}S_{\bar X} ,\bar X + t_{0.05/2(v)}S_{\bar X} \right)$$

99%的双侧置信区间: $$ \left(\bar X - t_{0.01/2(v)}S_{\bar X} ,\bar X + t_{0.01/2(v)}S_{\bar X} \right)$$

例2 已知某地27例健康成年男性血红蛋白量的均数为 X = 125 g/L ，标准差 S=15g/L ,试问该地健康成年男性血红蛋白量的95%和99%置信区间

本例n=27，S=15g/l

95%CI: $$ \left(\bar X ± t_{0.01/2(26)} {\frac{15}{\sqrt{27}}} \right) =125 ± 2.056*2.38$$ (119.06,130.94)g/L

99%CI: $$ \left(\bar X ± t_{0.01/2(26)} {\frac{15}{\sqrt{27}}} \right) =125 ± 2.779*2.38$$ (116.98,133.02)g/L

注意

例1中并不能说该市19岁健康男大学生的平均身高有95%的概率落在区间 (171.3,173.1)里! 这是由于平均身高作为总体均值，它是一个常数，因此这个常数要么在 区间(171.3,173.1)里，要么不在。也就是说，概率为0或1，不会出现其它的概 率值。 而这里的95%是说，对于一组随机样本，构造的置信区间(X -1.96sX ,X +1.96sX ) 在带入样本估计值之前，它的上下限都是随机变量，因此这实际上是一个随机 的区间，那么我们就可以说，总体均值落在这个随机区间的概率为95%。

三、总体概率的区间估计

总体概率的置信区间与样本含量 n、阳性频率 P 的大小有关， 可根据 n 和 P 的大小选择以下两种方法。

1. 正态近似法

当样本含量足够大，且 P 和 1­P 不太小，则样本率的分布近 似正态分布。 公式为:(P­-Z_α/2S_P ,P­-Z_α/2S_P ) P 为样本率， S_P为率的标准误的估计值。

例三：用某种仪器检查已确诊的乳腺癌患者94例，检出率为78.3%。 估计该仪器乳腺癌总体检出率的95%置信区间。

分析:本例样本例数较大，且样本率 P 不太小，可用正态近似法:

$$ P ± Z_{\alpha/2}S_{P} = P ± Z_{0.05/2}{\sqrt{\frac{P\left(1-P\right)}{n}}} = 0.783 ± 1.96 * {\sqrt{\frac{0.783\left(1-0.783\right)}{120}}} = (0.709,0.857)$$

2. 查表法

当 n 较小，如 n≤50，特别是 p 和 1­p 接近0或1时，应按照 二项分布的原理估计总体率的可信区间。

参考资料

中山大学课程 《医学统计学》方积乾