8. 因子分析
一、因子分析的思想
区别:
- 主成分分析通过线性组合将原变量综合成几个主成分
- 因子分析通过构筑若干意义较为明确的公因子
- 主成分分析是“变异数”导向的方法,
- 因子分析是“共变异数”导向的方法。
联系:
因子分析是主成分分析的推广
特点:
- 因子变量数远少于原变量数
- 因子变量是一种新的综合
- 因子变量之间没有相关关系
- 因子变量具有明确的解释性
用途:
- 减少分析变量个数;
- 通过对变量间关系探测,将原变量进行分类。
二、因子分析模型
基本思想:
- 将相关性较高的分在同一类中,每一类代表了一个基本结构, 即公因子。
- 用少数不可测的公共因子的线性函数来描述原观测的每一分量。
Q型与R型因子分析
- 样品间的因子分析称为Q型因子分析
- 变量间的因子分析称为R型因子分析

【例9.1】水泥行业上市公司经营业绩因子模型实证分析


三、因子载荷的估计及解释
极大似然估计法


主因子估计法


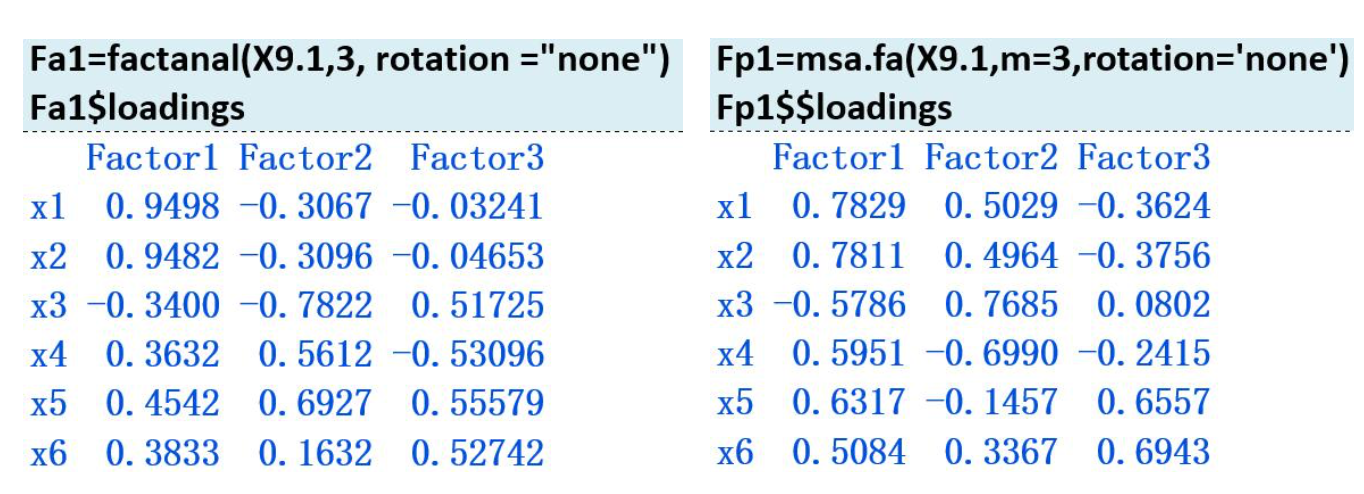
因子载荷的意义

方差贡献及共同度
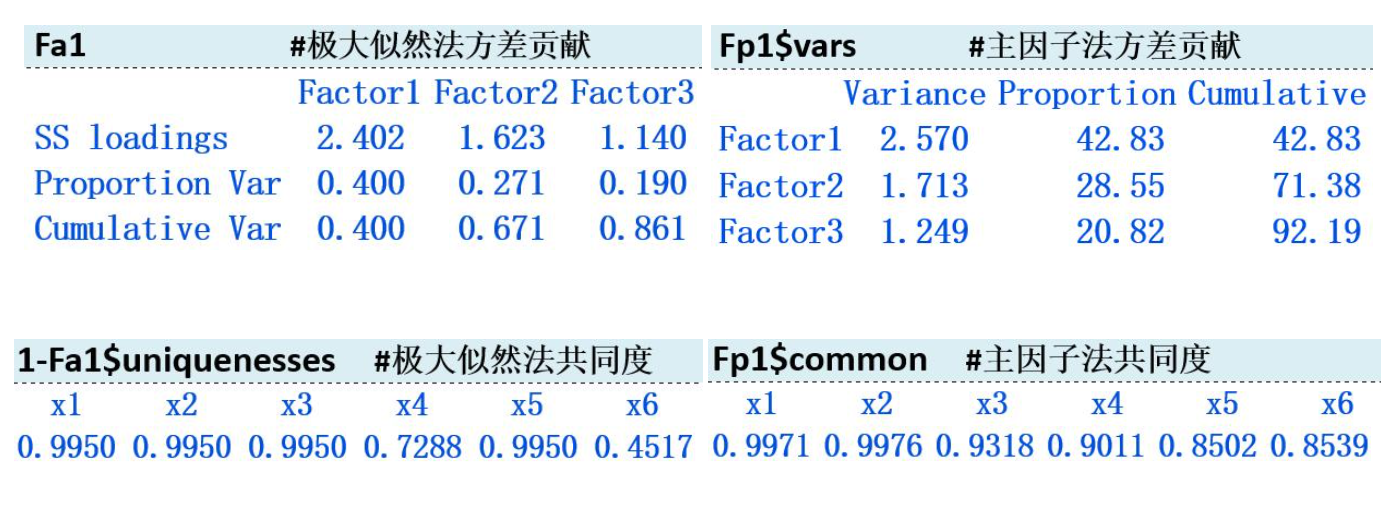
四、因子旋转
旋转目的
- 寻找每个主因子的实际意义
- 如果各主因子的典型代表变量不突出,就需要进行旋转
- 使因子载荷矩阵中载荷的绝对值向0和1两个方向分化
旋转方法


例子

五、因子得分

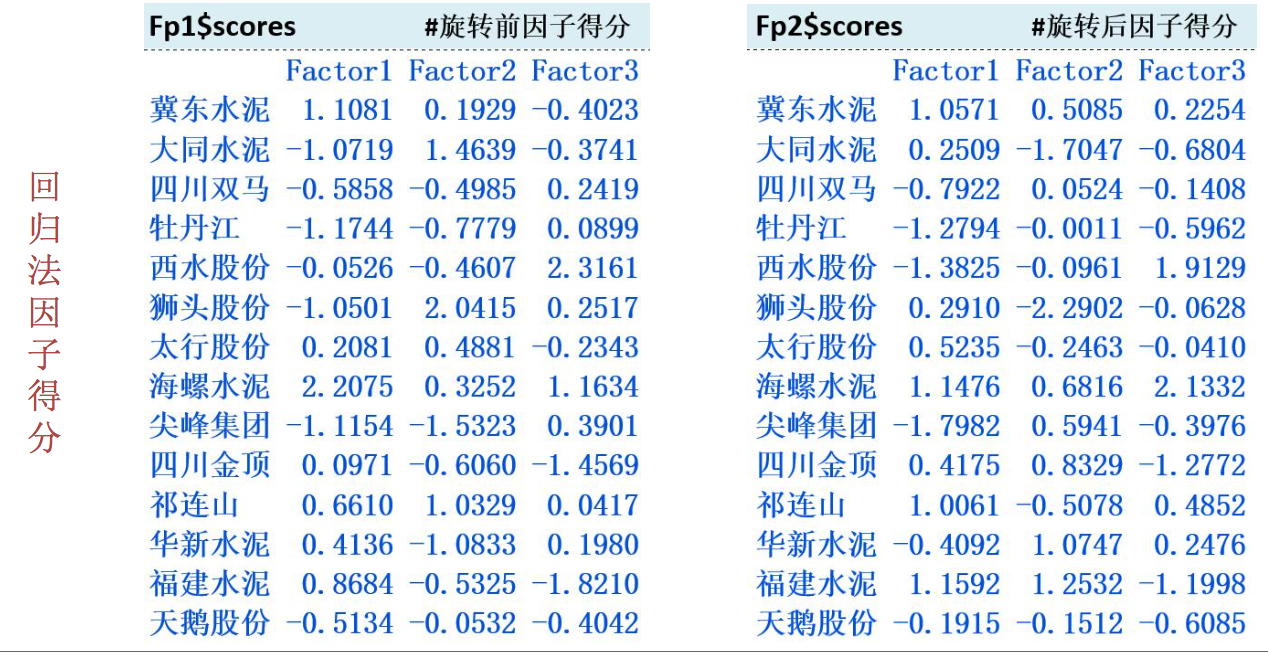

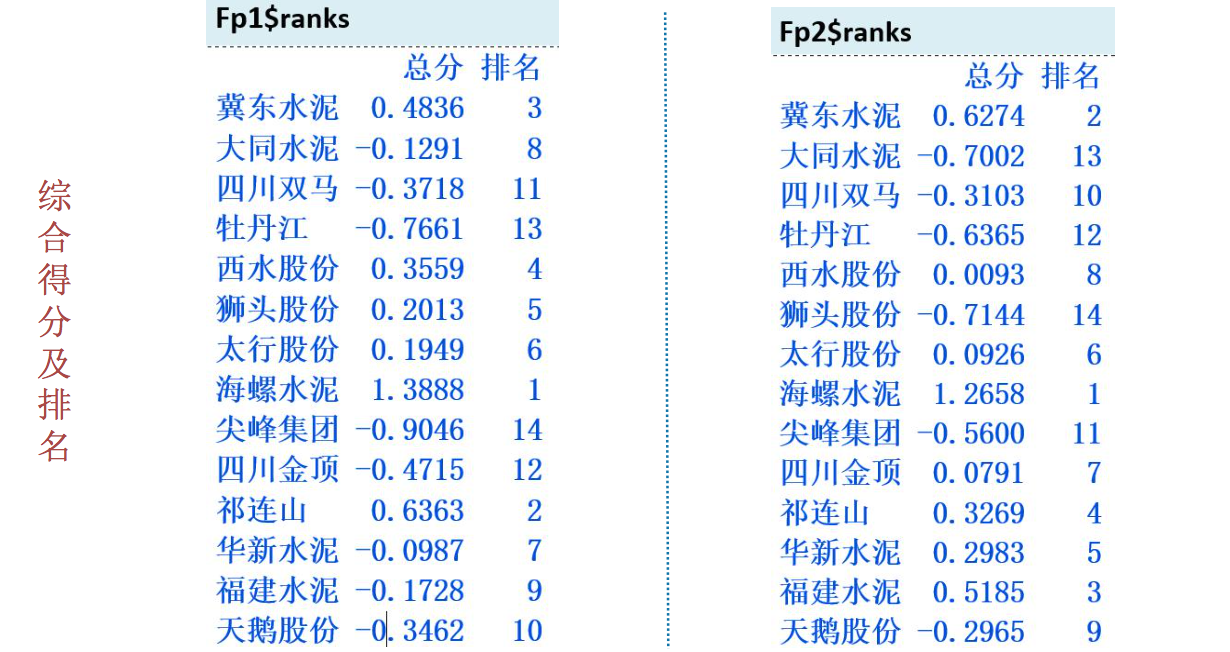
六、因子分析步骤

因子分析的基本步骤

R语言因子分析过程

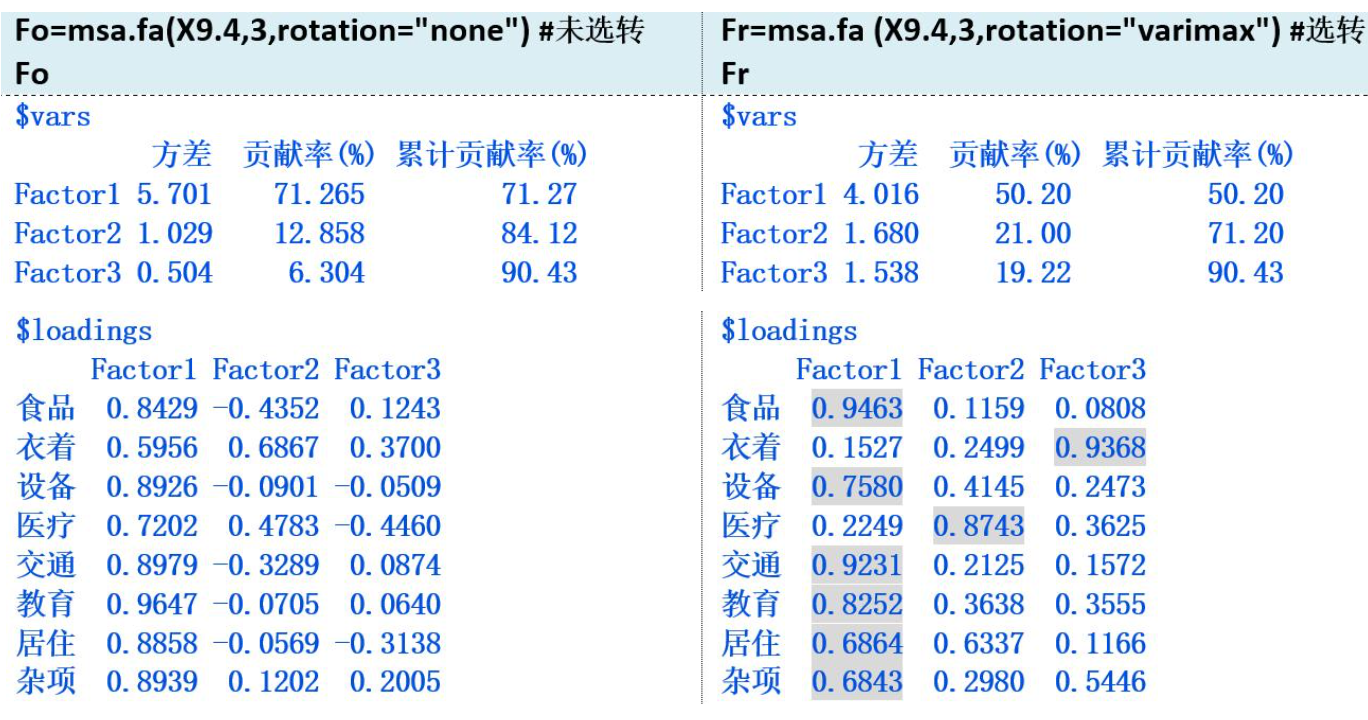


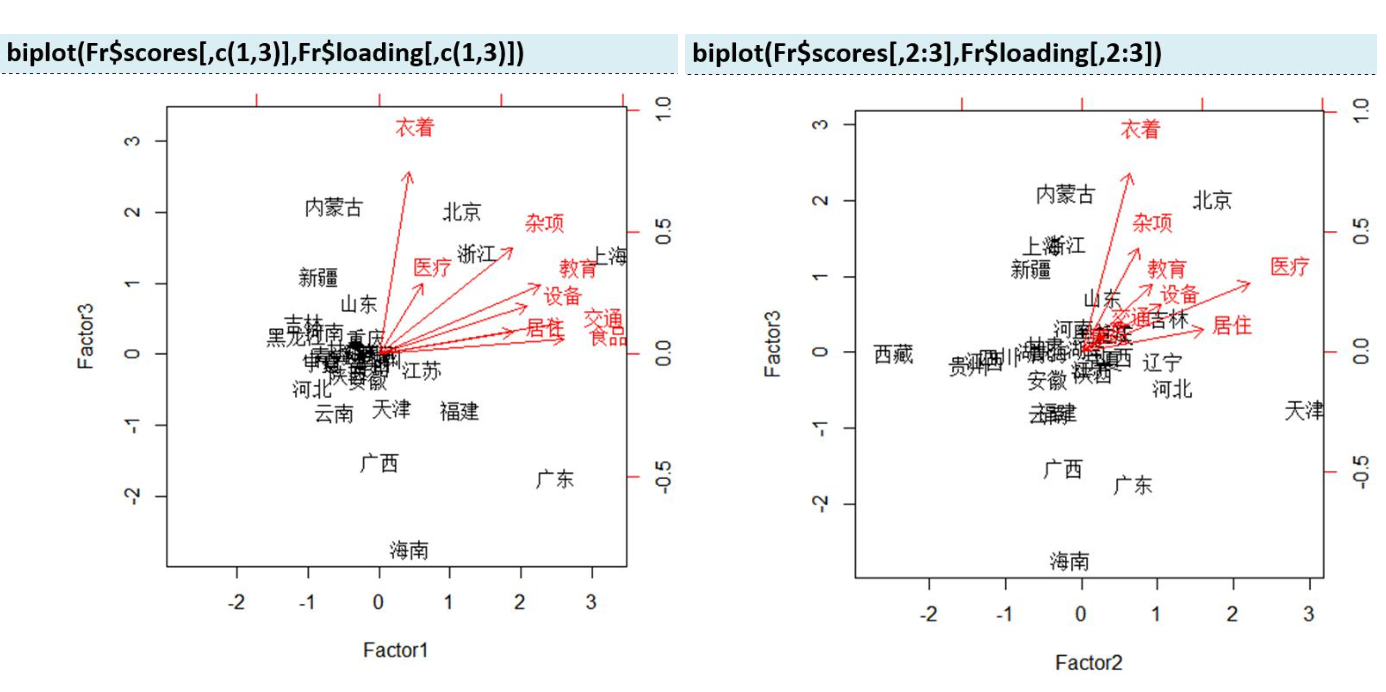
七、实际中如何进行因子分析
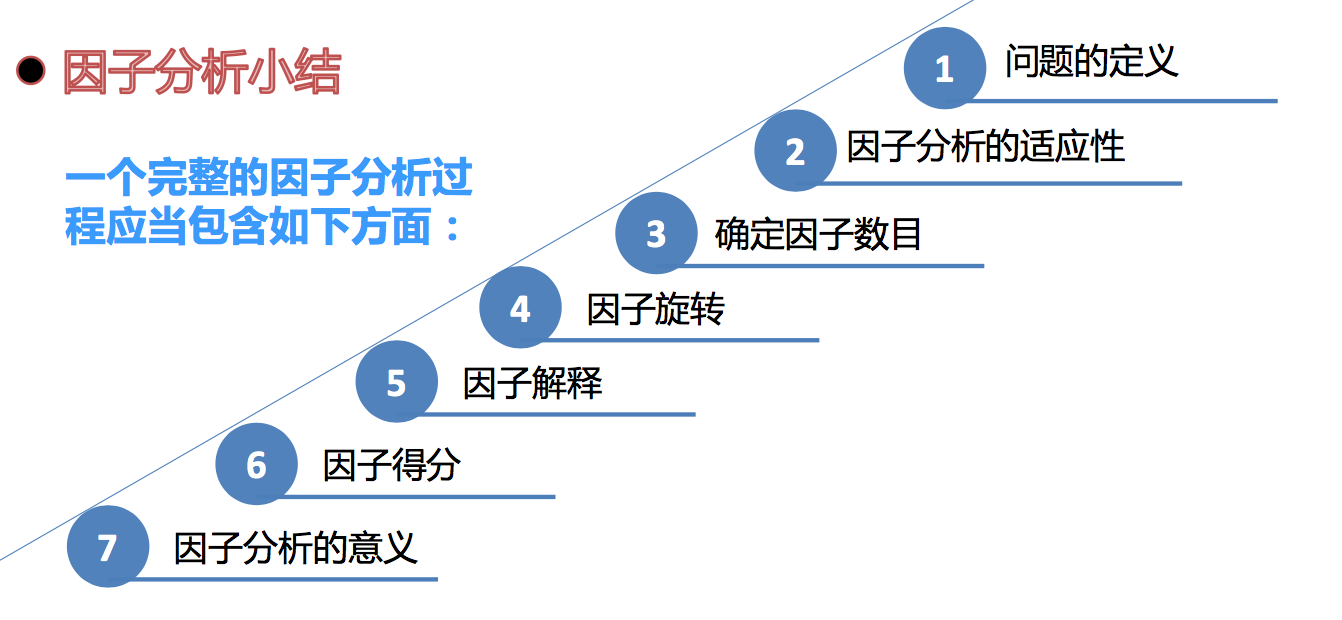
参考资料
暨南大学 王斌会老师 《多元统计分析及R语言建模》课件
这里是一个广告位,,感兴趣的都可以发邮件聊聊:tiehan@sina.cn
![]() 个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn
个人公众号,比较懒,很少更新,可以在上面提问题,如果回复不及时,可发邮件给我: tiehan@sina.cn

