排序【4】--CCA对应分析
一 CCA方法简介:
典范对应分析(canonical correspondence analusis, CCA),是基于对应分析发展而来的一种排序方法,将对应分析与多元回归分析相结合,每一步计算均与环境因子进行回归,又称多元直接梯度分析。其基本思路是在对应分析的迭代过程中,每次得到的样方排序坐标值均与环境因子进行多元线性回归。CCA要求两个数据矩阵,一个是植被数据矩阵,一个是环境数据矩阵。 首先计算出一组样方排序值和种类排序值(同对应分析),然后将样方排序值与环境因子用回归分析方法结合起来,这样得到的样方排序值即反映了样方种类组成及生态重要值对群落的作用,同时也反映了环境因子的影响,再用样方排序值加权平均求种类排序值,使种类排序坐标值值也简介地与环境因子相联系。其算法可由Canoco软件快速实现。
最大优点:CCA是一种基于单峰模型的排序方法,样方排序与对象排序对应分析,而且在排序过程中结合多个环境因子,因此可以把样方、对象与环境因子的排序结果表示在同一排序图上。
缺点:存在“弓形效应”。克服弓形效应可以采用除趋势典范对应分析(detrended canonical correspondence, DCCA).
结果可信性:查看累计贡献率及环境与研究对象前两个排序轴之间的相关性。
二、计算过程
现在我们举一个虚拟的计算例子:假使我们得到7个样方5个种的多度数据及两个环境因子的数据(张金屯 1995),有两个矩阵:
| 样方\种 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | ri |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0 | 1 | 0 | 2 | 0 | 4 |
| 2 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 3 |
| 3 | 0 | 2 | 0 | 1 | 0 | 1 | 0 | 4 |
| 4 | 3 | 0 | 0 | 1 | 1 | 0 | 2 | 7 |
| 5 | 1 | 1 | 2 | 0 | 0 | 1 | 0 | 5 |
| Cj | 5 | 3 | 3 | 3 | 2 | 4 | 3 |
矩阵2:
| 样 方\环境因子 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | 0.2 | 0.1 | 0.1 | 0.3 | 0.6 | 0.6 | 0.2 |
| 2 | 0.5 | 0.9 | 0.8 | 0.4 | 0.4 | 0.8 | 0.7 |
由于环境因子间的测量指标往往差别悬殊,一般需要对环境数据进行标准化,这里是一个简单的例子,我们将两个环境因子中心化得到新的矩阵:
| 样 方\环境因子 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 1 | -0.03 | -0.13 | -0.13 | 0.07 | 0.37 | -0.13 | -0.03 |
| 2 | -0.14 | 0.26 | 0.16 | -0.24 | -0.24 | 0.16 | 0.06 |
下面是CCA排序基本过程:
第一步,任意给定样方排序初始值:
(1, 2, 3, 4, 1, 2, 3 )
第二步,计算种类排序值,其是样方初始值的加权平均:
(2.25, 2.33, 2.5, 2.0, 2.2)
第三步,再用加权平均法求样方新值,得:
(2.09, 2.57, 2.24, 2.25, 2.17, 2.30, 2.11)
第四步,用多元回归分析计算样方排序值与环境因子间的回归系数,
用多元回归法计算样方与环境因子之间的回归系数bk,这一步是普通的回归分析,用矩阵形式表示为

关于矩阵运算见附录III。由最后一次迭代所求出的b称为典范系数(canonical coefficient),它反映了各个环境因子对排序轴所起的作用的大小,是一个生态学指标。
得:
b0=2.25, b 1=0.255, b2=0.655
第五步,计算样方排序新值zj(j= 1,2,…, N)
Z=Ub (9.37)
(9.37)是(9.35)的矩阵形式。
计算样方新值:比如
z 1=2.25+0.255×(-0.03)+0.655×(-0. 14)=2. 15
同法求得:
Z=(2.15, 2.38, 2.32, 2.11, 2.19, 2.32, 2.28)
第六步,对样方排序值进行标准化,同CA/RA和DCA(9.30~9.33)。
分别计算:

计算:V=2.42 S=0. 18
Z(a)=(1.06, 0.22, -0.56, -1.72, -1.28, -0.56, -0.78)
第七步,以Z(a)为基础回到第二步,重复以上过程,最后得到:7个样方在第一排序轴上的坐标:
0.059, -0.129, -0.078, 0.011, 0.098, -0.061, 0.113 (λ=0.269)
5个种在第一排序轴上的坐标:
0.010,0.054,-0.121,0.143,-0.144 (λ=0.269)
第八步,求第二排序轴:
第二排序轴的基本过程与第一轴一致,不同的是要进行正交化。而正交化方法与修正的CA/RA方法完全一致。所以,我们不再列出计算过程,只给出最终的结果。
7个样方在第二排序轴上的坐标为:
-0.053,0.017,0.065,-0.042,0.108,-0.062,0.060 (λ=0.18)
5个种在第二排序轴上的坐标为:
-0.130,0.252,0.040,-0.036,-0.028 (λ=0.18)
第九步:计算环境因子的排序坐标:
先求得以上得到的两个样方排序轴与环境因子间的相关系数akm得下表:
| 环境因子 | 第一排序轴 | 第二排序轴 |
|---|---|---|
| 1 | 0.630 | 0.383 |
| 2 | -0.720 | 0.125 |
再计算环境因子的坐标(9.38),比如,环境因子在第一坐标轴上的坐标
f11 = √(0.269*(1-0.269)) *0.630 = 0.279
同法可得:
f 12=0. 170,f2 1=-0.274,f22=0.047
第十步,绘双序图,为了便于图形表示,我们将上面求得的坐标值全部扩大 1000倍,绘得图9.21。 从图9.21我们知道,第一个环境因子与前两个排序轴都是强正相关;而第二个环境因子与第一轴是强负相关,与第二轴则是正相关,但关系不十分密切(因为其与第二轴的夹角很大)。从样方分布看,样方5和7与第一环境因子密切相关;样方2则与环境因子2有较密切的关系。种类分布也同样可做这样的解释。比如种3和环境因子2相关联。由于这个例子很简单,从原始数据矩阵我们就可以看到这些关系。
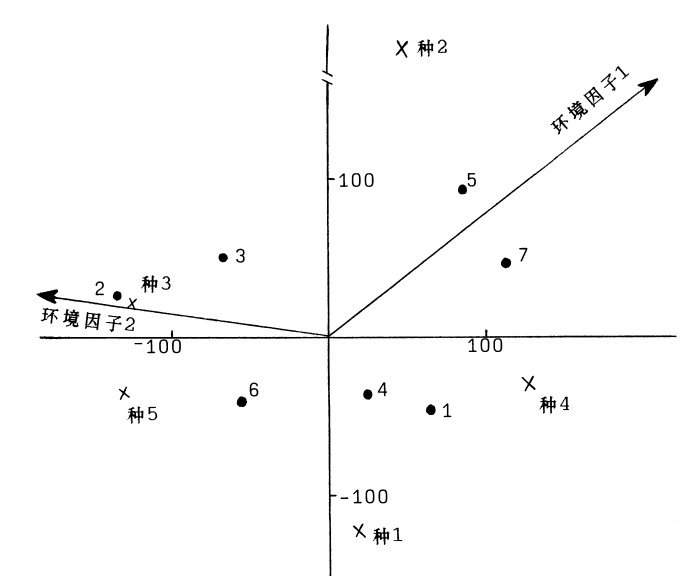
图9. 21 5个种7个样方和两个环境因子得CCA排序
反映植被类型与8个环境因子之间的关系,符号代表不同的群落类型:
(▲)碱性沼泽;(○)中性沼泽林地;(■)高位酸性沼泽.8个因子是:水深度(W),沼泽水的PH,传导性(Cond),沼泽水Fe、SiO2含量, 以及乔木总盖度(TC)和灌木总盖度(SC).
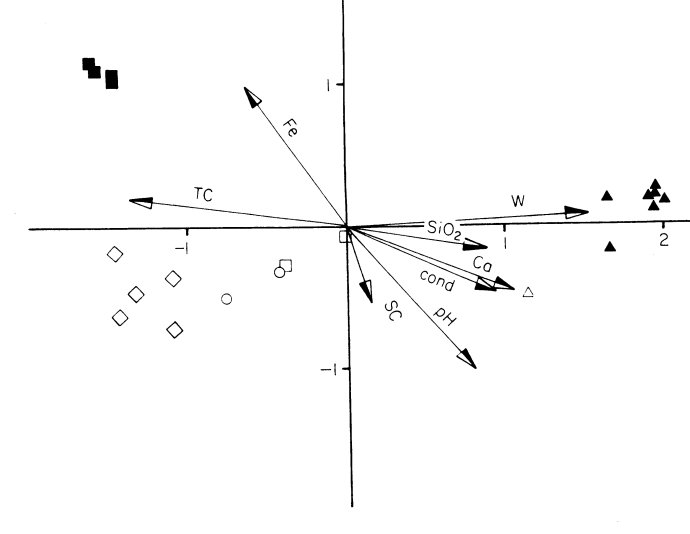
从图上可以看出, 植物群落的分布与水的深度、PH、Fe的含量及乔木总盖度有较为密切的关系。 CCA是以CA/RA为基础的,它存在CA/RA的缺点,即弓形效应。为了修正这一点,Braak(1987)又将CCA与DCA结合起来,产生一种叫除趋势典范对应分析(Detrended Canonical Correspondence Analysis,DCCA)的新方法,克服了弓形效应。
三、CCA排序图解释:
箭头表示环境因子,箭头所处的象限表示环境因子与排序轴之间的正负相关性,箭头连线的长度代表着某个环境因子与研究对象分布相关程度的大小,连线越长,代表这个环境因子对研究对象的分布影响越大。箭头连线与排序轴的夹角代表这某个环境因子与排序轴的相关性大小,夹角越小,相关性越高。
四、关键问题
(1)RDA或CCA的选择问题:RDA是基于线性模型,CCA是基于单峰模型。一般我们会选择CCA来做直接梯度分析。但是如果CCA排序的效果不太好,就可以考虑是不是用RDA分析。RDA或CCA选择原则:先用species-sample资料做DCA分析,看分析结果中Lengths of gradient 的第一轴的大小,如果大于4.0,就应该选CCA,如果3.0-4.0之间,选RDA和CCA均可,如果小于3.0, RDA的结果要好于CCA。
(2)计算单个环境因子的贡献率:CCA分析里面所得到的累计贡献率是所有环境因子的贡献率,怎么得到每个环境因子的贡献率:生成三个矩阵,第一个是物种样方矩阵,第二个是目标环境因子矩阵,第三个是剔除目标环境因子矩阵后的环境因子矩阵。分别输入Canoco软件中,这样CCA分析得到的特征根贡献率即是单个目标环境因子的贡献率。
参考资料
- 博客: http://blog.sciencenet.cn/blog-4981-27852.html
- 有个博客:http://www.yelinsky.com/blog/archives/225.html(里面提到用excel怎么作图)
- 张金屯老师数量生态学专第9章讲排序http://pan.baidu.com/s/1c0vjs1U(超赞的一个关于排序的讲解)
