【7.4】图的遍历

一、图的遍历 (graph traversal)

给出一个图G和其中任意一个顶点V0， 从V0出发系统地访问G中所有的顶点， 每个顶点访问而且只访问一次

• 深度优先遍历
• 广度优先遍历
• 拓扑排序

1.1 图遍历的考虑

从一个顶点出发，试探性访问其余 顶点，同时必须考虑到下列情况

• 从一顶点出发，可能不能到达所有其 它的顶点。 如 非连通图;
• 也有可能会陷入死循环。 如 存在回路的图

1.2 解决办法

• 为每个顶点保留一个 标志位 (mark bit)
• 算法开始时，所有顶点的标志位置零
• 在遍历的过程中，当某个顶点被访问时， 其标志位就被标记为已访问

1.3 图的遍历算法框架

二 深度优先遍历(depth-first search)

• 深搜(简称DFS) 类似于树的先根次序遍历，尽可能先对纵深方向进行搜索
• 选取一个未访问的点 v0 作为源点
• 访问顶点 v0
• 递归地深搜遍历 v0 邻接到的其他顶点
• 重复上述过程直至从 v0 有路径可达的顶点都已被访 问过
• 再选取其他未访问顶点作为源点做深搜，直到 图的所有顶点都被访问过

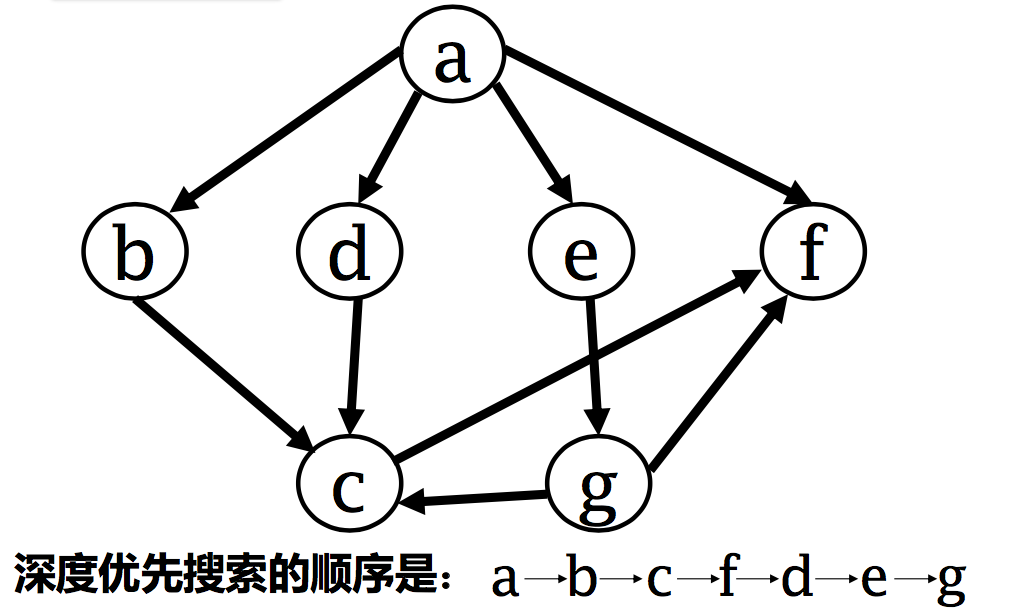
图的深度优先遍历 (DFS) 算法

三、广度优先遍历

广度优先搜索 (breadth-first search，简 称 BFS。其遍历的过程是:

• 从图中的某个顶点 v0 出发
• 访问并标记了顶点 v0 之后
• 一层层横向搜索 v0 的所有邻接点
• 对这些邻接点一层层横向搜索，直至所有由 v0 有路径 可达的顶点都已被访问过
• 再选取其他未访问顶点作为源点做广搜，直到所 有点都被访问过

图的广度优先遍历(BFS)算法：

图搜索的时间复杂度：

• DFS 和 BFS 每个顶点访问一次，对每一条边 处理一次 (无向图的每条边从两个方向处理)
• 采用邻接表表示时，有向图总代价为 Θ(n + e)， 无向图为 Θ(n + 2e)
• 采用相邻矩阵表示时，处理所有的边需要 Θ(n^2) 的时间 ，所以总代价为 Θ(n + n^2) = Θ(n^2)

四、拓扑排序

• 对于 有向无环图 G= (V，E) ，V 里顶点的线性 序列称作一个 拓扑序列，该顶点序列满足:

• 若在有向无环图 G 中从顶点 vi 到 vj 有一条路径， 则在序列中顶点 vi 必在顶点 vj 之前

• 拓扑排序 (topological sort)

• 将一个 有向无环图 中所有顶点在不违反 先决条件 关系 的前提下排成线性序列的过程称为 拓扑排序

4.1 拓扑排序方法

任何 有向无环图 (DAG) ，其顶点都可 以排在一个拓扑序列里，其拓扑排序的 方法是:

1. 从图中选择任意一个入度为0的顶点 且输出之
2. 从图中删掉此顶点及其所有的出边， 将其入度减少1
3. 回到第 (1) 步继续执行

用队列实现的图拓扑排序:

深度优先搜索实现的拓扑排序:

拓扑排序递归函数:

拓扑排序的时间复杂度:

• 与图的深度优先搜索方式遍历相同
• 图的每条边处理一次
• 图的每个顶点访问一次
• 采用邻接表表示时，为 Θ(n + e)
• 采用相邻矩阵表示时，为 Θ(n^2)

图算法需要考虑的问题:

• 是否支持
• 有向图、无向图
• 有回路的图
• 非连通图
• 权值为负
• 如果不支持
• 则修改方案?

递归与非递归的拓扑排序:

• 必须是有向图
• 必须是无环图
• 支持非连通图
• 不用考虑权值
• 回路
• 非递归的算法，最后判断 (若 还有顶点没有输出，肯定有回 路)
• 递归的算法要求判断有无回路

队列实现的拓扑排序讨论:

• 怎么知道图中所有顶点的入度?
• 是否可以用栈来取代队列?

深度优先搜索拓扑排序讨论:

• 对于起始点是否有要求?
• 是否可以处理有环的情况?

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾