【5.2】二叉树的抽象数据类型

抽象数据类型：

• 逻辑结构 + 运算
• 针对整棵树
• 初始化二叉树
• 合并两棵二叉树
• 围绕结点
• 访问某个结点的左子结点、右子结点、父结点
• 访问结点存储的数据

一、二叉树结点ADT

二、遍历二叉树

• 遍历 (或称周游，traversal)
• 系统地访问数据结构中的结点
• 每个结点都正好被访问到一次
• 二叉树的结点的 线性化

2.1 深度优先遍历二叉树

三种深度优先遍历的递归定义:

1. 前序法 (tLR次序，preorder traversal)。 访问根结点; 按前序遍历左子树; 按前序遍历右子树。
2. 中序法 (LtR次序，inorder traversal)。 按中序遍历左子树; 访问根结点; 按中序遍历右子树。
3. 后序法 (LRt次序，postorder traversal)。 按后序遍历左子树; 按后序遍历右子树; 访问根结点。

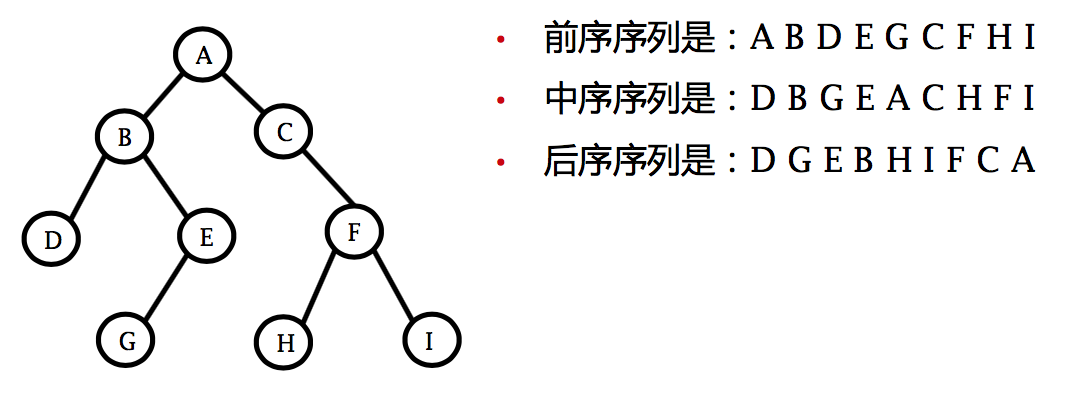
表达式二叉树:

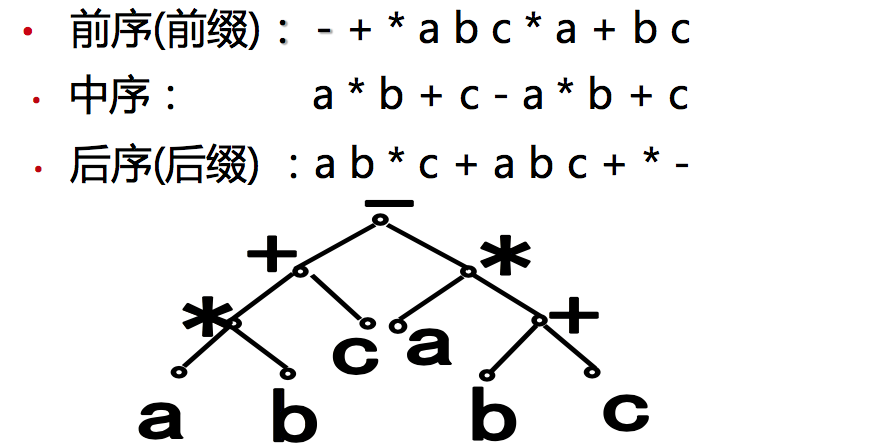
深度优先遍历二叉树(递归):

思考

前、中、后序哪几种结合可以恢复二叉树的结构?

已知某二叉树的中序序列为 {A, B, C, D, E, F, G}, 后序序列为 {B, D, C, A, F, G, E};,则其前序序列为 ____________________。

2.2 DFS遍历二叉树的非递归算法

• 递归算法非常简洁——推荐使用
• 当前的编译系统优化效率很不错了
• 特殊情况用栈模拟递归
• 理解编译栈的工作原理
• 理解深度优先遍历的回溯特点
• 有些应用环境资源限制不适合递归

非递归前序遍历二叉树

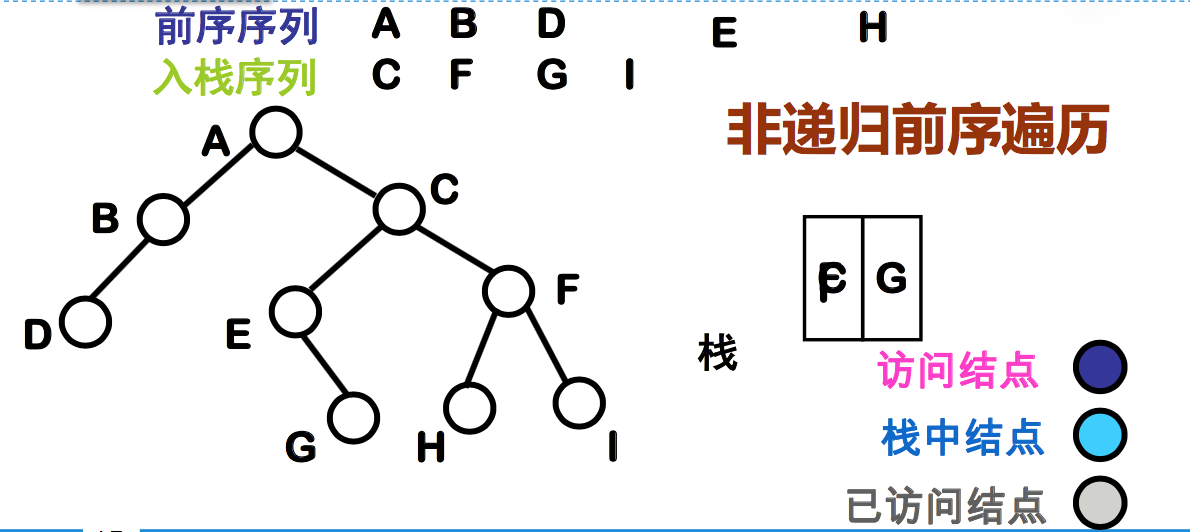
思想:

• 遇到一个结点，就访问该结点，并把此结点的非空右结点推入栈中，然后下降去遍历它的左子树;
• 遍历完左子树后，从栈顶托出一个结点，并按照它的右链接指示 的地址再去遍历该结点的右子树结构。

非递归中序遍历二叉树

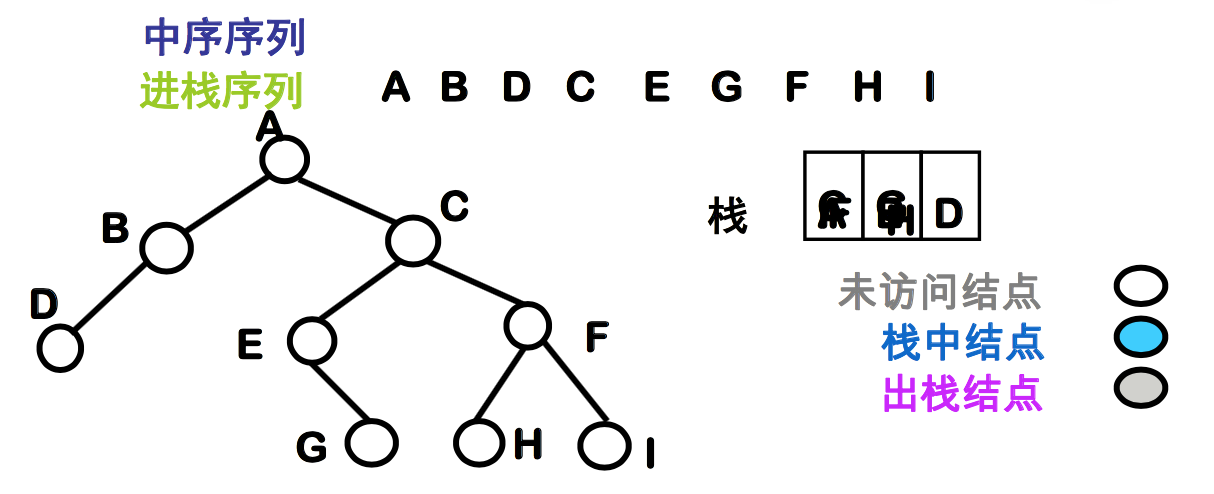
• 遇到一个结点
• 把它推入栈中
• 遍历其左子树
• 遍历完左子树
• 从栈顶托出该结点并访问之
• 按照其右链地址遍历该结点的右子树

非递归后序遍历二叉树

• 左子树返回 vs 右子树返回 ?
• 给栈中元素加上一个特征位
• Left 表示已进入该结点的左子树， 将从左边回来
• Right 表示已进入该结点的右子树， 将从右边回来

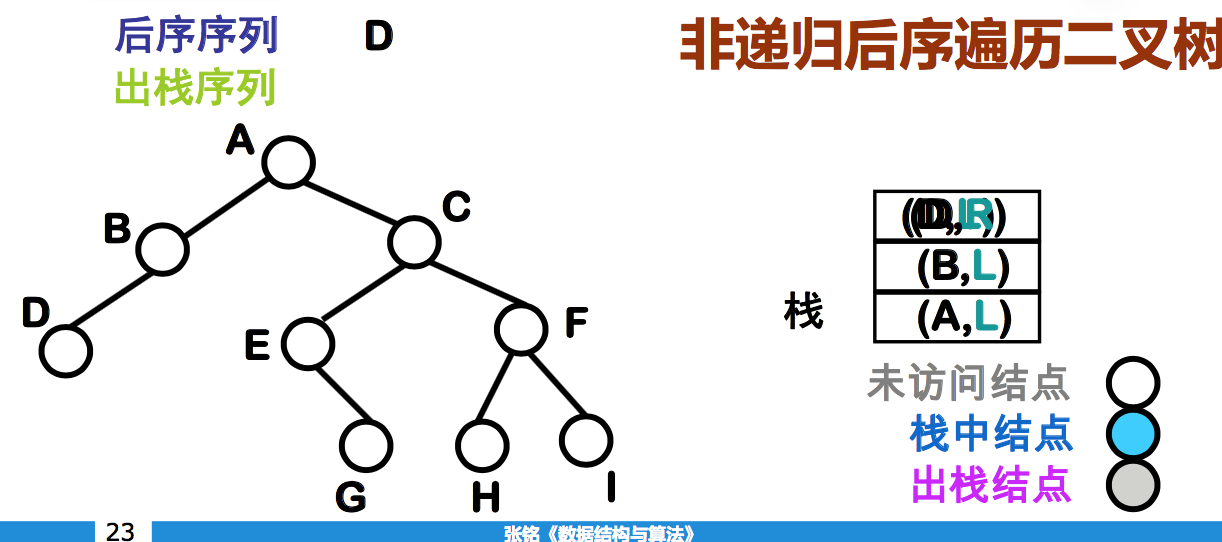
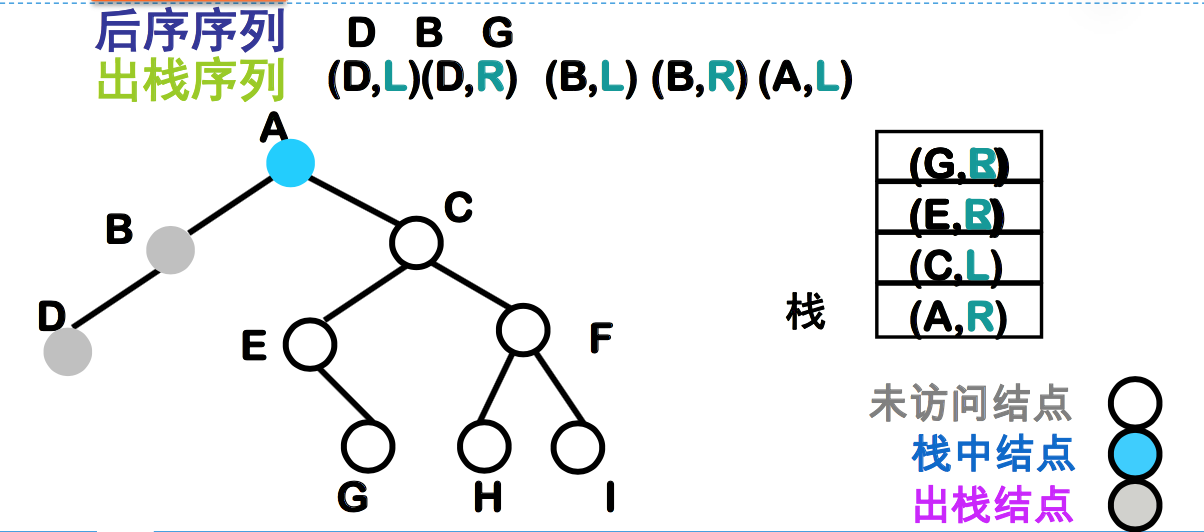
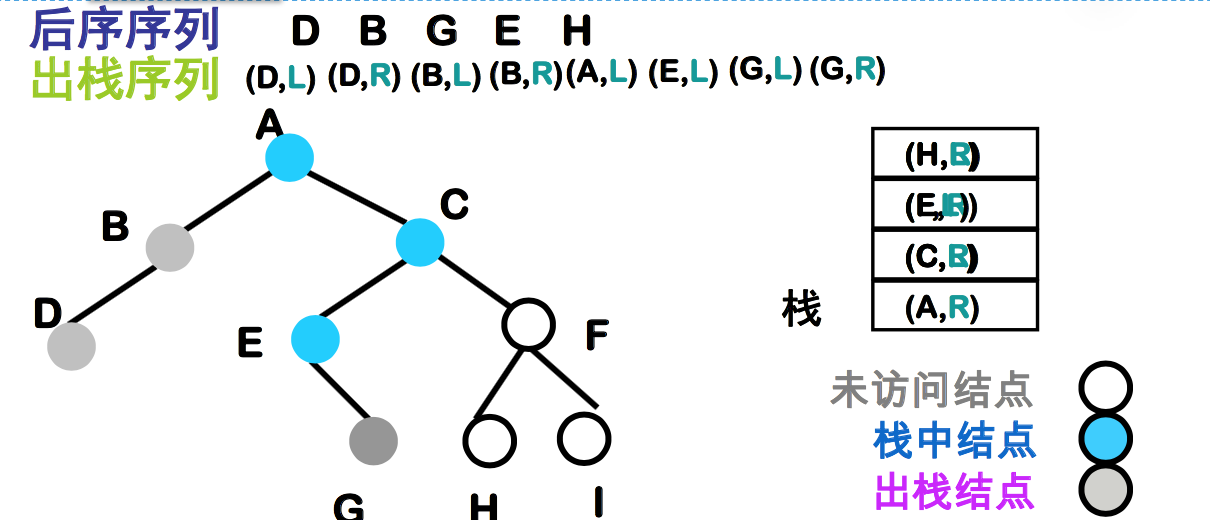
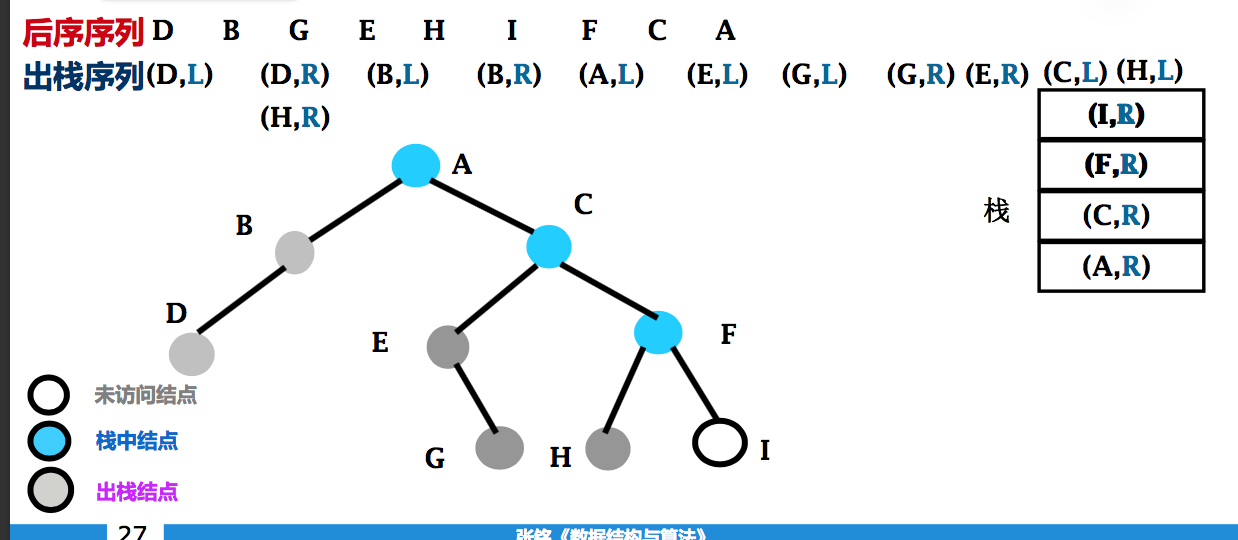
非递归后序遍历二叉树算法

二叉树遍历算法的时间代价分析

• 在各种遍历中，每个结点都被访问且 。只被访问一次，时间代价为O(n)
• 非递归保存入出栈(或队列)时间
• 前序、中序，某些结点入/出栈一次， 不超过O(n)
• 后序，每个结点分别从左、右边各入/出 一次， O(n)

深搜:栈的深度与树的高度有关

• 最好 O(log n)
• 最坏 O(n)

思考

• 非递归遍历的意义?
• 后序遍历时，栈中结点有何规律?
• 栈中存放了什么?
• 前序、中序、后序框架的算法通用性?
• 例如后序框架是否支持前序、中序访问?
• 若支持，怎么改动?

2.2 宽度优先搜索

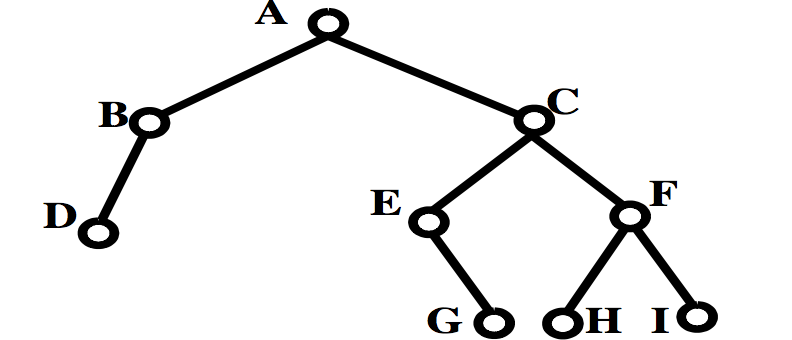
从二叉树的第 0 层(根结点)开始，自上至下 逐层遍历;在同一层 中，按照 从左到右 的顺序对结点逐一访问。

例如:A B C D E F G H I

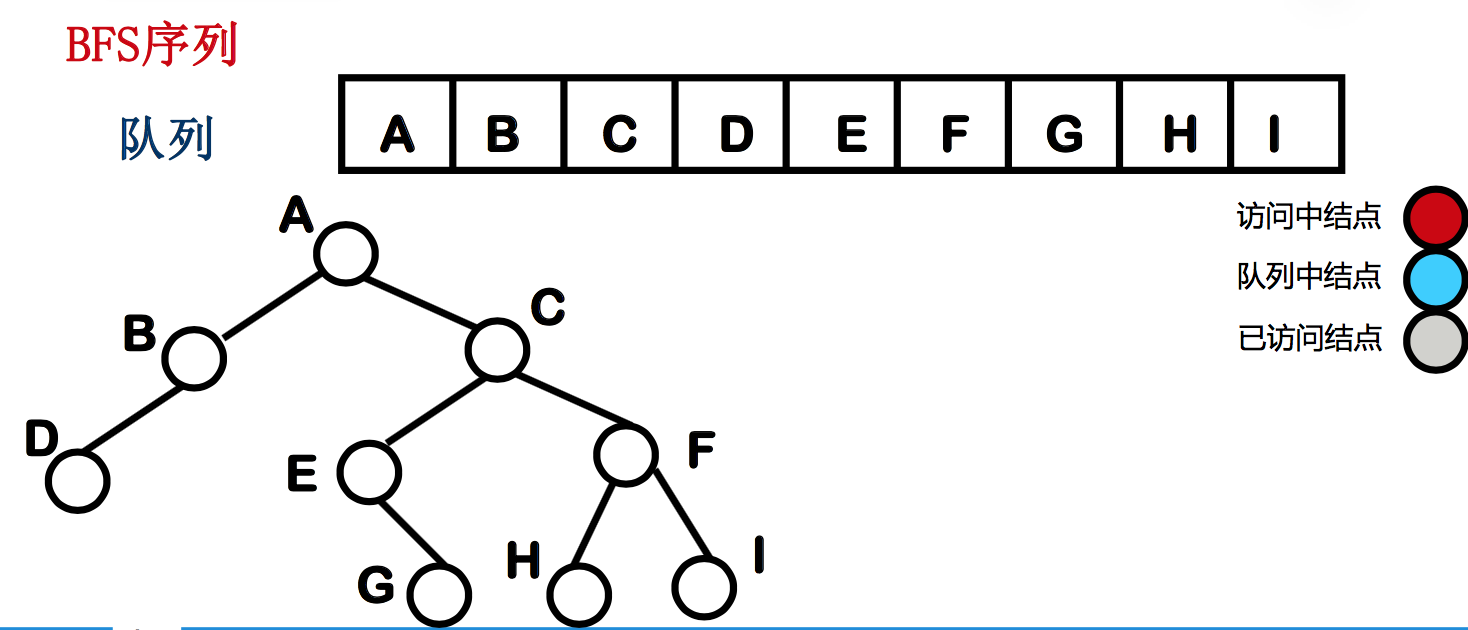
二叉树遍历算法的时间代价分析

• 在各种遍历中，每个结点都被访问且 只被访问一次，时间代价为O(n)
• 非递归保存入出栈(或队列)时间
• 宽搜，正好每个结点入/出队一次，O(n)
• 宽搜:与树的最大宽度有关
• 最好 O(1)
• 最坏 O(n)

思考

试比较宽搜与非递归前序遍历算法框架

参考资料

北京大学 《数据结构与算法》 张铭、赵海燕、宋国杰、黄骏、邹磊、陈斌、王腾