【4.5.1】验证曲线--欠拟合和过拟合
每个估算器都有其优点和缺点。 它的泛化误差(generalization error)可以根据偏差,方差和噪声进行分解。
- 估计量的偏差(bias)是不同训练集的平均误差
- 估计量的方差(variance)表明它对变化训练集的敏感程度
- 噪声(noise)是数据的属性。
这个例子说明了欠拟合和过度拟合的问题,以及我们如何使用多项式特征的线性回归来逼近非线性函数。 该图显示了我们想要近似的函数,它是余弦函数的一部分。 此外,还显示来自实际函数的样本和不同模型的近似值。 模型具有不同程度的多项式特征。 我们可以看到线性函数(度数为1的多项式)不足以拟合训练样本。 这被称为欠配合。 4阶多项式几乎完美地逼近真实函数。 然而,对于更高的度数,模型将过度拟合训练数据,即它学习训练数据的噪声。 我们通过使用交叉验证来定量评估过度拟合/欠拟合。 我们计算验证集上的均方误差(MSE)越高,模型从训练数据中正确推广的可能性越小。
在下图中,我们看到函数 $f(x)= \ cos(\frac {3} {2} \pi x)$和来自该函数的一些噪声样本。 我们使用三个不同的估计器来拟合函数:具有1度,4度和15度的多项式特征的线性回归。我们看到第一个估计器最多只能提供不适合样本和真实函数,因为它太简单了( 高偏差),第二个估计器几乎完美地逼近它,最后一个估计器完全逼近训练数据,但不能很好地拟合真实函数,即它对变化的训练数据(高方差)非常敏感。
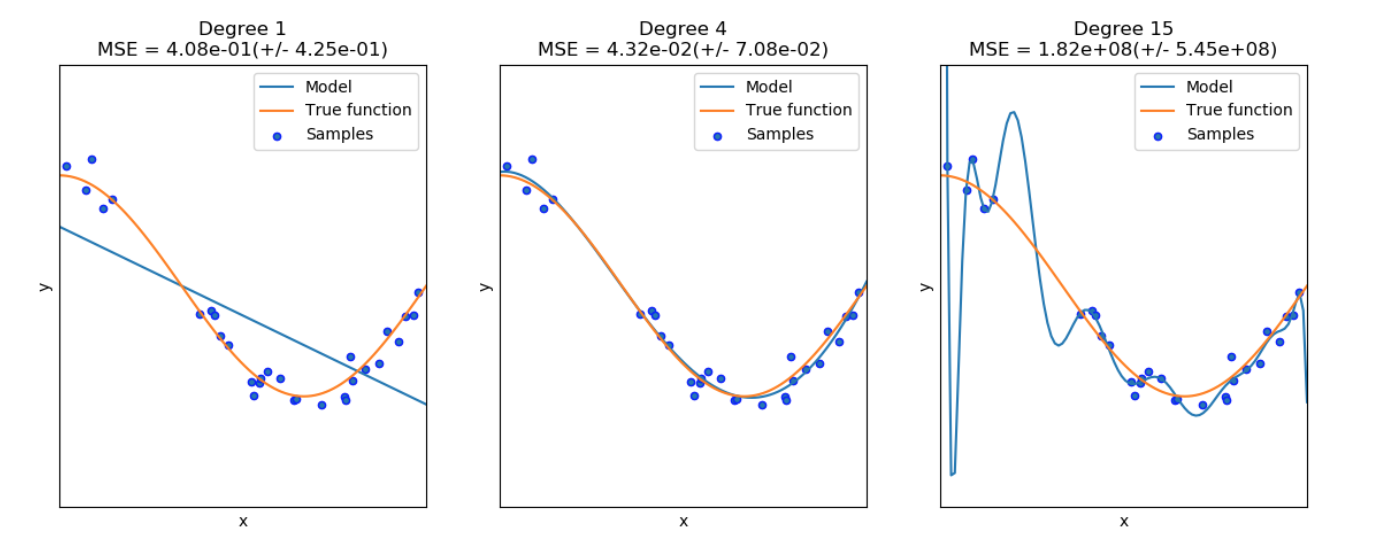
偏差和方差是估计量的固有属性,我们通常必须选择学习算法和超参数,以便偏差和方差都尽可能低(参见偏差 - 方差困境,Bias-variance dilemma)。 减少模型方差的另一种方法是使用更多的训练数据。 但是,如果真实函数过于复杂,无法通过方差较小的估算器进行近似,则应仅收集更多训练数据
在我们在示例中看到的简单的一维问题中,很容易看出估计器是否存在偏差或方差。 然而,在高维空间中,模型可能变得非常难以可视化。 因此,使用验证曲线与学习曲线描述的工具通常很有帮助
代码
print(__doc__)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
def true_fun(X):
return np.cos(1.5 * np.pi * X)
np.random.seed(0)
n_samples = 30
degrees = [1, 4, 15]
X = np.sort(np.random.rand(n_samples))
y = true_fun(X) + np.random.randn(n_samples) * 0.1
plt.figure(figsize=(14, 5))
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
polynomial_features = PolynomialFeatures(degree=degrees[i],
include_bias=False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X[:, np.newaxis], y)
# Evaluate the models using crossvalidation
scores = cross_val_score(pipeline, X[:, np.newaxis], y,
scoring="neg_mean_squared_error", cv=10)
X_test = np.linspace(0, 1, 100)
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
plt.plot(X_test, true_fun(X_test), label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x")
plt.ylabel("y")
plt.xlim((0, 1))
plt.ylim((-2, 2))
plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(
degrees[i], -scores.mean(), scores.std()))
plt.show()
参考资料
